They stand in clumps; they stand alone.
They flaunt themselves beside the Interstate; they lurk in the underbrush on distant hills.
They flower as full trees; they flower as bushes; they flower as single twigs stuck in the ground.
They clearly grow best in full sun; they obviously grow best in the shade.
In a 30-mile-or-so-square around Winchester VA, they grow *everywhere*. And they just happened to be at the peak of their blooming as we drove by last week.
There’s a poem in here somewhere, but a collage is faster. Here’s a summary of 1/100th of what we saw, just from the Interstate.

And here’s the thing: We were not in Oklahoma. So what, you ask. So this, I respond: The redbud is the state tree of Oklahoma. Methinks they should have more redbud than Virginia, which is hard to imagine.
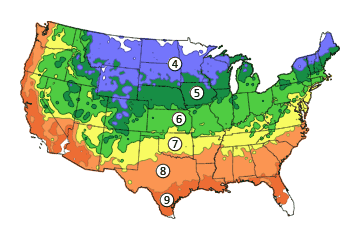
And here’s the other thing: They grow in hardiness zones 4 through 9. Where’s that, you ask. Everywhere in America, I respond.
And here’s the last thing: They’re Canadian. Yes, the American Redbud is actually Cercis canadensis. In Canada, they’re native only to Pelee Island (our southernmost point, roughly the same latitude as Northern California), but they grow elsewhere with some care, and you can buy one from these helpful folks.
What? Are you still here? Don’t let the Americans have all the fun. Get out and plant your very own redbud today.